JS-Sort算法示例中数据结构和算法的详细说明

排序算法介绍

排序也称为排序算法。排序是按指定顺序排列一组数据的过程。

分类分类

1)内部排序：是指将所有需要处理的数据加载到内存中进行排序。

2)外部排序法：的数据太大，无法加载到内存中，需要通过外部存储(文件等)进行排序。).

常见排序算法的分类

算法的时间复杂度测量程序(算法)执行时间的两种方法

1.事件后统计的方法这种方法是可行的，但是有两个问题：一是要评估设计的算法的运行性能，需要实际运行程序；

第二，获得时间的统计取决于环境因素，例如计算机的硬件和软件。如果在同一台计算机的相同状态下运行，该方法可能比该算法更快。

2.预估计方法通过分析算法的时间复杂度来确定哪种算法更好。

时频

时间频率：算法花费的时间与算法中执行的语句数成正比。算法中执行的语句越多，花费的时间就越多。算法中执行的语句数称为语句频率或时间频率。写成T(n)。

示例-基本情况

例如，为了计算从1到100的所有数字的总和，我们设计了两种算法：

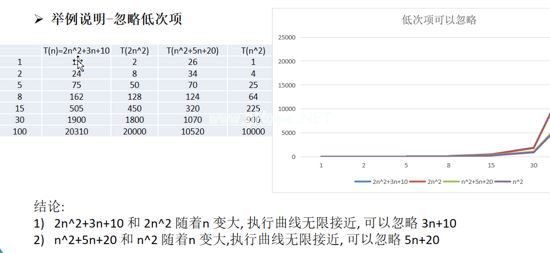
时间复杂性

1.一般来说，算法中基本运算语句的重复执行次数是问题规模n的函数，用T(n)表示。如果有一个辅助函数f(n)，使得T(n)/f(n)的极限值是n趋近于无穷大时不等于零的常数，那么f(n)就是与T(n)同数量级的函数。T (n)=o (f (n))，o (f (n))称为算法的渐进时间复杂度，简称时间复杂度。

2.T(n)不同，但时间复杂度可能相同。例如，T(n)=n7n6和T(n)=3n N2有不同的T(n)，但时间复杂度相同，为o (n)。

3.计算时间复杂度的方法：

通常使用常数1代替所有加法常数t (n)=n7n6=t (n)=n7n1，以仅保留最高阶项t (n)=n7n1=t (n)=n，并移除最高阶项t (n，T(n)=n=T(n)=n=O(n，n)的系数

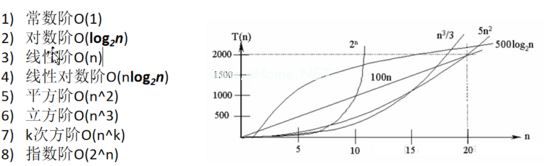
描述：

常见算法的时间复杂度如下：(1)<(log2n)<(n)<(nlog2n)<(n ^ 2)<(n ^ 3)<(n ^ k)<

从图中可以看出，我们应该尽可能避免使用指数算法

时间复杂度介绍示例1)常数阶O(1)

不管代码执行多少行，只要没有循环这样复杂的结构，代码的时间复杂度就是O(1)

上面的代码在执行时，其消耗并不会随着某个变量的增加而增加，所以无论代码有多长，即使有几万行，其时间复杂度也可以用O(1)来表示。

2)对数O阶(对数2 n)

说明：while循环中，我每次都乘以2，相乘后我离n越来越近，我们假设循环x次后我大于2，然后循环退出，也就是说2的x次方等于n，那么x=log 2 n，也就是循环log 2 n次后，代码结束。因此，该代码的时间复杂度为O(log 2 n)。O的2(log 2n)根据代码随时间变化。如果i=i * 3，则为O(log 3 n)。

3)线性顺序O(n)

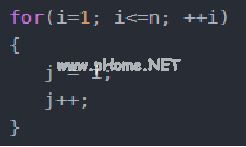
注意：这个代码，for循环中的代码会被执行N次，所以它消耗的时间随着N的变化而变化，所以这类代码可以用O(n)来表示它的时间复杂度

4)线性对数O阶(nlogN)

注：线性对数O阶(nlogN)其实很好理解。如果时间复杂度为O(logn)的代码循环N次，那么它的时间复杂度为n * O(logN)，也就是O(nlogN)

5)平方O (n)阶

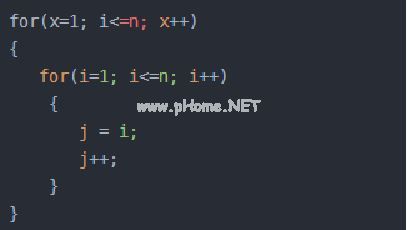
注：O(n)的平方阶更容易理解。如果O (n)的代码被嵌套并再次循环，其时间复杂度为O (n)。这段代码实际上嵌套了两层N个循环，其时间复杂度为O(n*n)，即O(n)如果将O (n)层循环的N改为M，其时间复杂度变为O (m *)

6)三次o (n)，k次幂o (n，k)

注：只参考上面O (N)，相当于三层N循环，其他类似

平均时间复杂度和最差时间复杂度是指当所有可能的输入实例以相等的概率出现时算法的运行时间。最坏的时间复杂度叫做最坏的时间复杂度。通常，所讨论的时间复杂度是最坏情况下的时间复杂度。究其原因，最差情况下的时间复杂度是算法在任何输入实例上运行时间的极限，保证了算法的运行时间不会比最差情况下更长。平均时间复杂度是否与最差时间复杂度一致取决于算法(如图3360所示)。

算法的空间复杂度的引入类似于时间复杂度的讨论。算法的空间复杂度定义为算法消耗的存储空间，也是问题规模n的函数，空间复杂度是算法在运行过程中临时占用的存储空间的度量。一些算法占用的临时工作单元数量与解题规模n有关，n随着n的增加而增加，当n较大时，会占用更多的存储单元，如快速排序和合并排序算法。从用户体验的角度来看，程序执行的速度更为重要。一些缓存产品(redis、memcache)和算法(基数排序)的本质是用空间换取时间。

摘要

以上是边肖介绍的JS中数据结构和算法的详细说明，希望对大家有所帮助。如果你有任何问题，请给我留言，边肖会及时回复你。非常感谢您对我们网站的支持！如果你觉得这篇文章对你有帮助，请转载，请注明出处，谢谢！